Элементарные функции что это
Элементарные функции и их графики
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
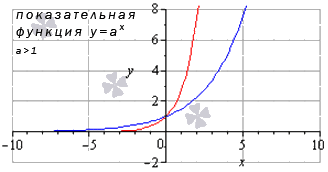
2. Показательные
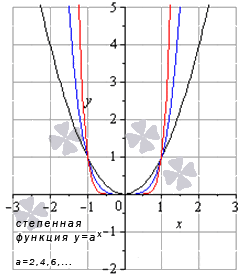
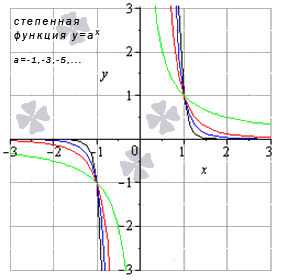
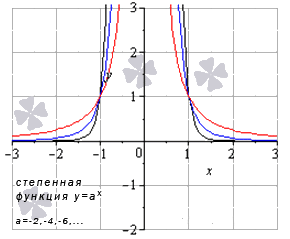
Это функции вида y = a x
4. Тригонометрические
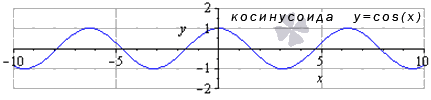
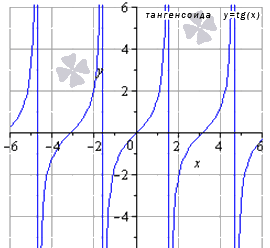
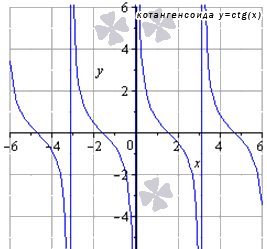
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x 2 · e x — произведение квадратичной и показательной функций; y = sin(a x ) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.
| a > 1 |  | |||
| 0 1 |  | |||
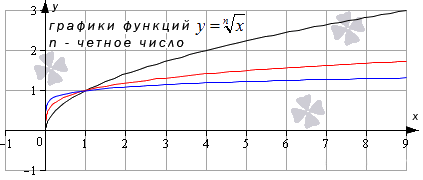
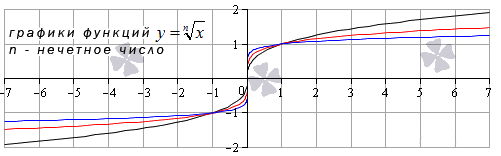
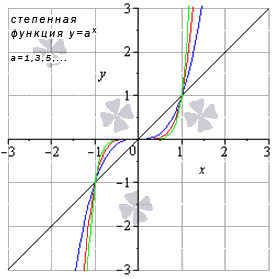
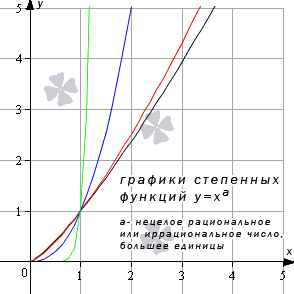
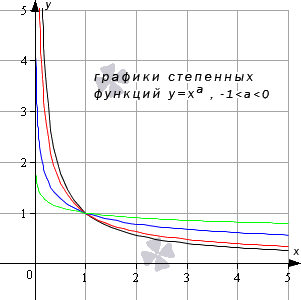
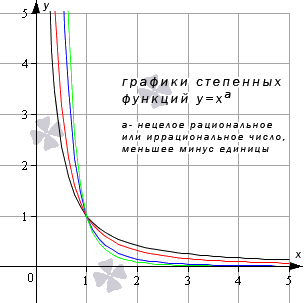
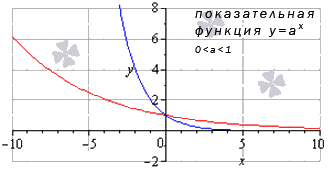
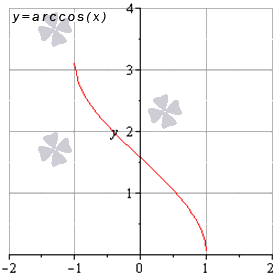
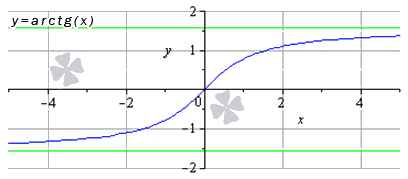
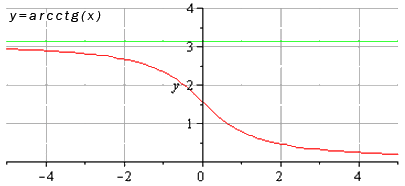
| 0 2 + 5? Об этом — статья «Преобразования графиков функций». Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций. Почему в уравнении 3 x = 3 5 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3 x возрастает и каждое значение принимает только один раз. Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически. Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки». Основные элементарные функции: их свойства и графикиОсновные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов. Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства. Выделяют следующие виды основных элементарных функций: Постоянная функция
Свойства постоянных функций: Корень n-й степениДанная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы). Рассмотрим две вариации функции.
Похожий вид у графиков функции четной степени при иных значениях показателя. Свойства функции корень n-ой степени, n – четное число
Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида. Свойства функции корень n-ой степени, n – нечетное число Степенная функцияВид графиков и свойства функции зависят от значения показателя степени. Степенная функция при нечетном положительном показателе
Свойства степенной функции, когда показатель степени – нечетный положительный Степенная функция при четном положительном показателе
Свойства степенной функции, когда показатель степени – четный положительный: Степенная функция при нечетном отрицательном показателе
Свойства степенной функции, когда показатель степени – нечетный отрицательный: Степенная функция при четном отрицательном показателе степени
Свойства степенной функции, когда показатель степени – четный отрицательный: Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)
Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика. Свойства степенной функции при 0 a 1 : Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)
Иные значения показателя степени а при условии a > 1 дадут похожий вид графика. Свойства степенной функции при a > 1 : Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)
Показательная функцияСначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).
Свойства показательной функции, когда основание меньше единицы: Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).
Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции. Свойства показательной функции, когда основание больше единицы: Логарифмическая функцияГрафик логарифмической функции имеет различный вид, исходя из значения основания а.
Иные значения основания, не большие единицы, дадут аналогичный вид графика. Свойства логарифмической функции, когда основание меньше единицы: Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).
Иные значения основания больше единицы дадут аналогичный вид графика. Свойства логарифмической функции, когда основание больше единицы: Тригонометрические функции, их свойства и графикиТригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики. В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль. График данной функции называется синусоида.
Свойства функции синус: График данной функции называется косинусоида.
Свойства функции косинус: График данной функции называется тангенсоида.
Свойства функции тангенс: График данной функции называется котангенсоида.
Свойства функции котангенс: Обратные тригонометрические функции, их свойства и графикиОбратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.
Свойства функции арксинус:
Свойства функции арккосинус:
Свойства функции арктангенс:
Свойства функции арккотангенс: Классификация элементарных функцийВыделяют множество видов элементарных функций, каждый из которых обладает собственным набором свойств. Так, одни можно дифференцировать на определенном промежутке бесконечное число раз, другие являются непрерывными, ортогональными и др. В этой статье мы расскажем об общепринятой классификации элементарных функций. Что такое элементарные функцииНачнем с базового определения. Элементарные функции – это такие функции, которые получаются из основных функций с помощью сложения, вычитания, умножения и деления, а также посредством преобразования сложных функций. Таким функции бывают: В свою очередь алгебраические функции можно разделить на иррациональные и рациональные (целые рациональные и дробные рациональные). Рассмотрим каждый вид функций отдельно. Понятие алгебраических функцийАлгебраические функции – это функции, которые состоят из цифр и букв, соединяющихся друг с другом при помощи знаков сложения, вычитания, умножения, деления, извлечения корня и возведения в целую степень. Иными словами, это те функции, которые можно получить из основных функций f ( x ) = x и f ( x ) = 1 и любых чисел, проведя с ними необходимые алгебраические действия (вычитание, умножение, сложение, деление и др.) Выделяют рациональные и иррациональные алгебраические функции. Рациональные функции – это те, в которых аргумент не находится под знаком корня (радикала). Они в свою очередь делятся на целые рациональные (т.е. многочлены) и дробные рациональные (выражения, составленные из многочленов). Иррациональные функции – это те, которые содержат в себе аргумент под знаком корня (радикала). Понятие трансцендентных функцийПрочие функции, которые нельзя отнести к алгебраическим, относятся к виду трансцендентных. Трансцендентные функции – это те, которые образуются при помощи логарифмирования, возведения в иррациональную степень или с помощью тригонометрических и обратных тригонометрических преобразований. Функции и графикиИзучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике – функции полезности, издержек, функции спроса, предложения и потребления. в радиотехнике – функции управления и функции отклика, в статистике – функции распределения. Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». и/или по ссылке Построение графиков, содержащих модуль аргумента или модуль функции, а также сумму или разность нескольких модулей. С 17.04.21 до экзаменв просмотр по кнопке ОТКРЫТ. | ||||
| Степенная | y = x 3 |  | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Движение графиков функций». |
| Степенная | y = x 1/2 |  | График функции y = √x | Самый простой случай для дробной степени (x 1/2 = √x). Случаи с коэффициентами изучаются в разделе «Движение графиков функций». |
| Показательная | y = a x |  | График показательной функции | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5 x (a = 1/2 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). |
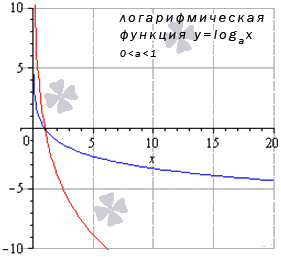
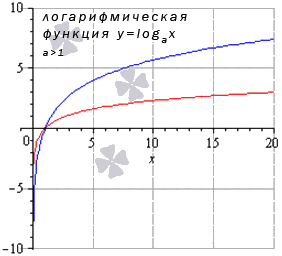
| Логарифмическая | y = logax |  | График логарифмической функции | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 На сервере youtube.com открыт канал Mathematichka, на котором размещаются видео, связанные с изучением графиков функций и экзаменационными задачами на эту тему. Подписывайтесь и пишите в комментариях свои вопросы и пожелания. Пример такого видео. |
| Перейти на главную страницу. | ||||
 |
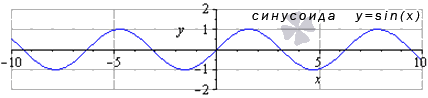
, где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.
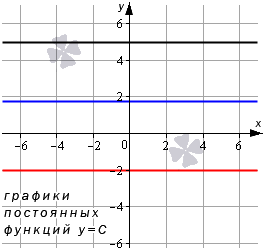
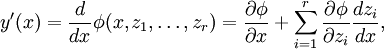
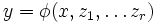сам является элементарной функцией, то он представим в виде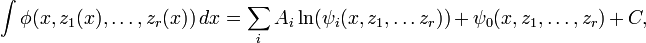
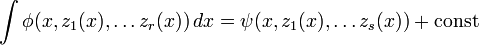
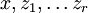и т. д. Функции 
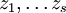являются алгебраически независимыми и удовлетворяют некоторой системе дифференциальных уравнений вида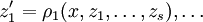
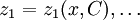— семейство решений этой системы, то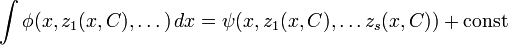
,
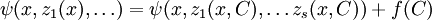
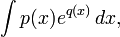
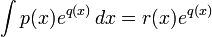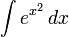
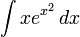
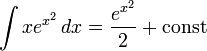
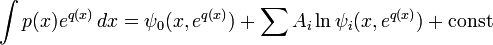
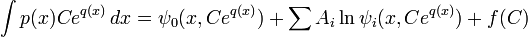
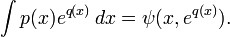
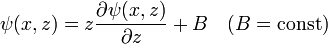
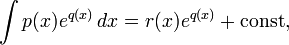
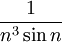. [3]