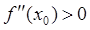что означает минимум и максимум

Что такое максимум и минимум?

Что такое максимум и минимум?

— Получать максимум от общения.

— Чтобы выучить стихотворение его нужно прочесть как минимум 3-4 раза.

— Максимум на что он способен, это…..

— У них есть как минимум два общих друга.

— Он получил максимальный бал.

— Используй возможности по-максимуму!

— Это тот минимум, который нужно знать.

— Минимальное атмосферное давление.

— Минимальные/максимальные холода за ….. лет.

— Вам потребуется минимум несколько часов для выполнения этой работы.

Такие понятия как максимум и минимум можно встретить и в специальных научных терминах. Например, в математике есть такое понятие как максимум и минимум функции.

Таким образом, максимумом в математике называется наибольшее значение функции. При этом максимальное значение функции больше всех соседних с ней значений. Максимум функции – это такое ее значение, когда сначала значение увеличивается, а затем сразу же начинает убывать, при этом она имеет максимум в том месте, где увеличение и уменьшение функции переходят от одного к другому. Минимум функции – это, соответственно, наименьшее значение функции.

Первую производную функции можно считать положительной, если она поднимается вверх, когда мы увеличиваем переменную, тогда функцию можно считать положительной. Если же первая переменная при увеличении производного, убывает, то функцию следует считать отрицательной.

Производная – это основное значение, которое используют при дифференциальных вычислениях (изучение производной и дифференциала, которые помогают исследовать математические функции), она может пониматься как скорость изменения функции в конкретной точке. Чем скорость больше, тем сильнее меняется функция, чем меньше, тем медленнее (это, однако, правда, только если функция положительная). Таким образом, именно скорость изменения функции в заданной точке и определяет ее наклоны и выпуклости. А переменная – это величина, которая способна менять свое значение. Ее обозначают как x или time.

Переменной можно считать атрибут системы (как физической, так и абстрактной), который способен изменить свое значение. В более глобальном смысле переменной можно назвать и время, и температуру и, вообще, всю жизнь (они могут меняться). Переменная имеет множество значений, которые она способна принимать. Можно считать, что это множество и является переменной.

Что касается непосредственно функции, то она должна пройти от положительного к отрицательному значению через ноль. Таким образом, при том значении переменного, которому соответствует максимум функции, ее производная будет равна нулю. Именно это свойство функции позволяет определять значения x, при которых функция достигает максимума. Однако, если мы увеличим переменную и, при этом, функция сначала увеличивается, а затем уменьшается, то функция, при изменении с отрицательного значения на положительное (пройдя через ноль), достигнет не максимального, а, наоборот, минимального значения. Хотя по логике вещей это можно было бы принять именно за максимальное значение (он находится в верхней точке функции).

Точки максимума и минимума функции еще называют точками экстремума.

Таким образом, как в обычной жизни, так и в математике максимум и минимум – это две крайние противоположности, которые обозначают что-то самое большое и что-то самое маленькое.

Источник

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.

\(- 9\): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции \(y=3x^5-20x^3-54\).
Решение:
1. Найдем производную функции: \(y’=15x^4-60x^2\).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является \(-2\).

Источник

Максимум и минимум функции

Определение.Точка х₀ называется точкой максимума(точкой минимума) функции , если существует такая δ-окрестность точки х₀, что для всех из этой окрестности выполняется неравенство .

Рисунок 1. – Точка максимума.	Рисунок 2. – Точка минимума.

Определение.Значение функции в точке максимума (точке минимума) называется максимумом (минимумом) функции.

Определение. Максимум и минимум функции называются экстремумами функции.

Теорема(необходимое условие экстремума – НУЭ).

Если дифференцируемая функция имеет экстремум в точке х₀, то ее производная в этой точке равна нулю: .

Геометрически равенство означает, что в точке экстремума дифференцируемой функции касательная к ее графику параллельна оси Ох.

Обратная теорема неверна, т. е. если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Например, производная функция 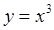точке равна нулю, однако в этой точке функция имеет только перегиб, а не экстремум.

Замечание. Непрерывная функция может иметь экстремум только в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.

Теорема(достаточное условие экстремума – ДУЭ-1).

Если непрерывная функция у=f(x) дифференцируема в некоторой окрестности критической точки х₀ (за исключением, быть может, самой точки х₀) и при переходе через нее слева направо производная f ¢ (x) меняет знак с «+» на «–», то х₀ есть точка максимума, а с «–» на «+», то х₀ – точка минимума.

Исследовать функцию на экстремум означает найти все ее экстремумы. Из теорем НУЭ и ДУЭ-1 вытекает следующая схема исследования функции на экстремумы:

1) найти область определения функции;

2) найти производную функции;

3) найти критические точки функции;

4) выбрать из них только те, которые являются внутренними точками области определения функции;

5) исследовать знак производной 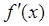слева и справа от каждой из выбранных критических точек;

6) в соответствии с теоремой ДУЭ-1 выписать точки экстремума (если есть);

7) вычислить значение функции в найденных точках экстремума.

Пример.Найти экстремумы функции .

Решение: исследуем функцию по приведенной выше схеме.

1) .

2) .

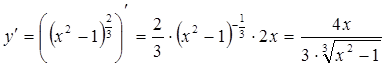
3) Решим уравнение , т.е. . Получим , .

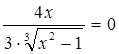
4) Точки, подозрительные на экстремум: , , , т.к. исходная функция определена в точках .

5) Исследуем знак производной:

6) – точки минимума, – точка максимума;

7) , .

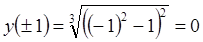
Иногда бывает удобным использовать другой достаточный признак существования экстремума, основанный на определении знака второй производной.

Теорема (достаточное условие экстремума – ДУЭ-2).

Если в точке первая производная функции равна нулю , а вторая производная в точке существует и отлична от нуля , то при в точке функция имеет максимум и минимум – при .

Источник